图片源于:https://www.nature.com/articles/s41612-025-00915-2
本研究使用了一个月度地表温度(LST)数据集,该数据集具有5600米的空间分辨率,覆盖了2003年至2014年期间。
该数据集通过建立一个回归分析模型,结合了中分辨率成像光谱仪(MODIS)数据和地面气象站的测量数据进行了重建。
该数据集没有缺失值,同时减少了云层覆盖的影响。
与原始MODIS LST数据相比,组合的数据集具有更高的准确性,且这些数据集已广泛应用于作为评估气候模型的参考。
在这里,我们也利用它来评估WRF模型的性能。
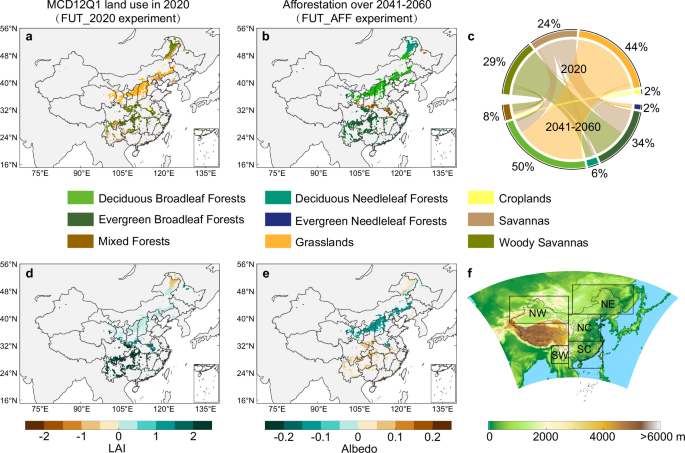
为了研究未来林业的影响,使用了三种土地覆盖数据集:WRF中的默认土地覆盖、2020年MCD12Q1土地覆盖数据集以及未来林业情景土地覆盖数据集。
WRF中的默认土地覆盖来自2001年MODIS土地覆盖类型产品,但未能准确描述中国的地表特征。
因此,本研究更新并使用了最新的2020年MODIS土地覆盖类型数据集(MCD12Q1),该数据集的空间分辨率为500米,时间分辨率为年间隔。
该产品提供了一种17类国际地球生物圈计划(IGBP)分类方案,并且能够良好匹配WRF的前17种土地利用类型。
MCD12Q1产品质量较高,全球整体准确性约为75%,已广泛用于气候建模研究作为下界条件。
未来林业情景数据集来自Song等人的研究,映射了中国未来潜在的林业区域分布。
与之前的理想化和假设性林业情景数据集相比,该土地覆盖数据集考虑了国家林业政策和气候变化影响的影响,展现了更为合理的林业发展潜力。
具体而言,中国国家林业局发布的《国家森林管理规划》(2016-2050)中提供了每个省份的未来植树造林面积。
为了研究气候变化对潜在森林分布的影响,使用了霍尔德里奇生物区模型。
该数据集中,在2041年至2060年期间,根据SSP2-4.5情景,中国的总植树造林面积为736400平方公里,基本符合国家林业规划的要求。
该数据集的空间分辨率为25公里,可以很好地与WRF模型匹配,确保了每个省份的造林面积符合国家森林管理规划,且造林范围与森林气候适宜性相匹配。
因此,未来的植树造林情景较为接近现实。
在本研究中,我们使用了两组初始和侧向边界条件(LBCs)数据集(ERA5重分析和MPI-ESM1-2-HR模型)来驱动WRF模型。
ERA5重分析数据集由欧洲中期天气预报中心(ECMWF)开发,已广泛应用于历史WRF模拟。
所需变量包括从1000hPa到50hPa的五个大气场(温度、地势高度、比湿度、东西风和南北风),共28个垂直层次,以及11个表面场(地表温度、海表温度、地表压力、海冰覆盖、海平面气压、土壤温度、土壤湿度、近地表温度、相对湿度、东西风和南北风),空间分辨率为1.0° x 1.0°,间隔为6小时。
来自马克斯普朗克研究所的6小时MPI-ESM1-2-HR模型输出数据用于驱动WRF模型进行未来的数值模拟,提供了CMIP6模型的边界条件。
MPI-ESM1-2-HR模型相较于其他CMIP6模型,在模拟五个WRF所需的大气场方面表现更好,因此在中国的动态下调中得到了推荐。
对于单变量模拟(即温度和降水)及大尺度环流场,MPI-ESM1-2-HR模型也表现出更高的优越性。
因此,MPI-ESM1-2-HR模型及其最新版本(MPI-ESM-MR)已广泛应用于未来区域气候建模作为边界条件。
与ERA5重分析数据一致,MPI-ESM1-2-HR模型的大气和表面场字段也已一致。
我们对原始MPI-ESM1-2-HR模型进行了0.9375°x 0.9375°的空间分辨率插值,以匹配ERA5,采用双线性插值法。
对于这两组边界条件,历史模拟的重点是1994-2014年期间,而2040-2060年期间被视为未来的预测模拟时期。
本研究选择的SSP2-4.5情景反映了一条中等的社会经济发展道路,同时放射性强迫在2100年达到4.5 W m−2的峰值。
在此情景中,各国保持当前的发展趋势,与一个相对雄心勃勃的减排未来一致,但社会、经济和技术趋势未会显著偏离历史模式。
因此,SSP2-4.5情景接近国家的现行承诺和相对现实的全球气候情景。
虽然MPI-ESM1-2-HR模型表现较其他GCM相对优越,但仍然存在一定的偏差。
因此,我们在考虑气候平均和方差的情况下,采用了来自Song等人的偏差修正方法,来修正MPI-ESM1-2-HR数据。
ERA5数据作为参考被用来校正MPI-ESM1-2-HR模型。
偏差修正的简要描述如下:
Hcor=DGCM_H×SDERA/SDGCM+MERA
Fcor=DGCM_F×SDERA/SDGCM+MERA+(MGCM_F-MGCM_H)
其中,Hcor和Fcor是历史基线(1994-2014)和未来时期(2040-2060)中6小时偏差修正的MPI-ESM1-2-HR模型。
DGCM_H和DGCM_F代表异常。
SDERA和SDGCM分别表示ERA5和MPI-ESM1-2-HR模拟在历史期间内的标准偏差。
SDERA/SDGCM表示方差调整项。
MERA代表ERA5数据的气候学平均值,(MGCM_F-MGCM_H)则表示基于MPI-ESM1-2-HR模拟的未来气候变化的平均值。
因此,偏差校正后的MPI-ESM1-2-HR模型的6小时均值和方差与ERA5重分析一致。
这种偏差修正方法应用于所有大气和表面场。
为了研究未来植树对地表温度的影响,采用了天气研究与预报(WRF)模型(版本4.2),这是一个耦合的陆地-大气区域气候模型。
WRF模型由多个机构(如国家海洋和大气管理局)和大学(如俄克拉荷马大学)联合开发。
作为一个先进的、非静态和开源的模型,WRF模型已被广泛用于研究区域气候模拟和陆气相互作用。
具体而言,WRF模型在模拟中国历史地表温度气候方面表现优于观测。
模型域覆盖整个中国及其周边地区。
模拟配置包括25公里的水平分辨率,垂直方向有40个层次,东西方向有289个网格,南北方向有212个网格。
物理参数化方案包括WSM 3类简单冰微物理方案、CAM长波和短波辐射方案、Grell-Devenyi对流方案、Noah-MP陆面方案以及YSU边界层方案。
WRF模型的模拟配置和参数化方案在中国显示出更好的性能。
本研究调查了WRF模型在中国历史时期(1995-2014)模拟地表温度的性能。
结果表明,嵌套偏差修正的MPI-ESM1-2-HR模型能够合理地再现地表气候的空间模式,并相较于参考观测数据表现良好。
此外,我们根据分位数映射(QM)方法修正了未来降水在FUT_2020和FUT_AFF实验中的偏差。
结果表明,QM偏差修正的降水(WRF-QM)能够明显减少历史模拟偏差。
同时,通过WRF-raw与WRF-QM比较未来植树诱导的降水变化。
为了研究未来植树的生物物理效应,我们设计了五个21年的数值实验(实验设计参见补充表2)。
历史模拟从1994年至2014年进行,分为两组历史实验(HIS_ERA和HIS_MPI)。
HIS_ERA实验采用了2001年的默认土地覆盖地图和ERA5分析数据集作为边界条件。
HIS_MPI实验与HIS_ERA实验保持相同的配置,但边界条件设置为偏差修正的MPI-ESM1-2-HR模型。
未来模拟从2040年到2060年进行,分为三组未来实验(FUT_2001、FUT_2020和FUT_AFF)。
FUT_2001和FUT_2020实验使用了默认和2020年MCD12Q1土地覆盖。
在未来植树(FUT_AFF)实验中,土地覆盖为未来植树情景,而其他设置与FUT_2020一致。
对于每个模拟,前一年因旋转时间被丢弃,剩余的20年模拟(1995-2014和2041-2060)被进一步分析。
我们分析了HIS_MPI与HIS_ERA实验相对观测的模拟性能。
HIS_MPI与HIS_ERA实验之间的差异表示由边界条件产生的偏差,因为WRF固有的偏差是相同的。
FUT_AFF与FUT_2020之间的差异(FUT_AFF减去FUT_2020)只能归因于未来植树引起的地表温度变化(ΔLST_aff)。
FUT_2001与HIS_MPI(FUT_2001减去HIS_MPI)之间的差异可投射出相对于历史时期(ΔLST_ssp245)的SSP2-4.5情景下地表温度的未来变化,代表了由于温室气体浓度增加而引起的全球变暖效应。
同时,我们还重新估计了考虑未来植树的地表温度(ΔLST_ssp245+aff,ΔLST_ssp245与ΔLST_aff之和)。
为测试差异的统计显著性,采用了0.01、0.05和0.1的显著性水平的Student’s t检验。
植树造林可以改变地表能量平衡,从而影响区域温度。
为了调查其机制,我们使用了分解温度度量(DTM)方法来量化地表能量通量中哪一项主导了地表温度的变化。
DTM方法由Juang提出,并已成功应用于温度响应与地表能量预算的归因分析。
在这里,地表能量平衡理论上表示为:
SWDN-SWUP+LWDN-LWUP=SH+LH+G
其中,SWDN和SWUP分别表示向下和向上的短波辐射,LWDN和LWUP表示向下和向上的长波辐射,而SH、LH和G分别表示显热、潜热和地面热通量。
享有LST_s的LWUP也可以通过斯特藩-博尔兹曼定律获得:
LWUP=εσLST_s^4
其中,LST_s是参考地表温度,ε是表面发射率,σ是斯特藩-博尔兹曼常数,等于5.67×10^{-8}Wm^{-2}K^{-4}。
在此,我们可以结合方程(3)和方程(4)得到:
εσLST_s^4=SWDN-SWUP+LWDN-SH-LH-G
然后通过应用泰勒级数展开,我们得到植树引起的地表温度变化:
ΔLST_s=1/(4εσLST_s^3)(ΔSWDN-ΔSWUP+ΔLWDN-ΔSH-ΔLH-ΔG)
在此,Δ表示灵敏度与对照实验(FUT_AFF减去FUT_2020)之间的变化。
因此,ΔLST_s可以通过计算方程(6)中的五个项的和来获得,而由于植树造林引起的实际地表温度变化(ΔLST_a)可以在这两个实验之间进行模拟。
请注意,ΔLST_s与ΔLST_a略有不同,前述差异在以往研究中同样存在。
这表明DTM方法中的误差。
这些误差来自高阶导数和人为热通量,难以量化。
尽管存在误差,但DTM方法主要可用于量化由于植树造成的各个表面能量预算成分变化的相对贡献。
此外,该方法与表面能量变化密切相关,因此仅能反映植树信号的局部效果。